Central Bank and 12 Regional Feds: Manipulating Today’s Economy (Page 2/3)
September 8, 2015
Akira Kondo
 Paul Volcker, the former Fed Chairman, at Fudan University in Shanghai, China in May 2012.
Monetary Policy
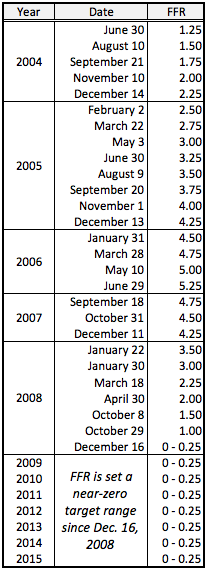
During 2008 when the U.S. economy was suffering from the global financial crisis, the FOMC was in full swing throughout the year to manipulate its economy to mitigate the damage from sever financial meltdown while its key three-month interest rates were gradually lowered from 4.25 percent to the zero interest policy on each FOMC meeting (Also read: Yield Curve). Such action is called, “expansionary monetary policy,” to stimulate the nation’s economy. On the other hand, contractionary monetary policy was operated during the mid-2000s when the housing bubble started to heat up. Today, the economy is under the zero interest policy while nearing full employment. The Fed may soon start to hike its key interest to cool down economy by operating the contractionary monetary policy. However, its action is not really a contractionary policy. It is rather normalizing the economy. Dual Mandate
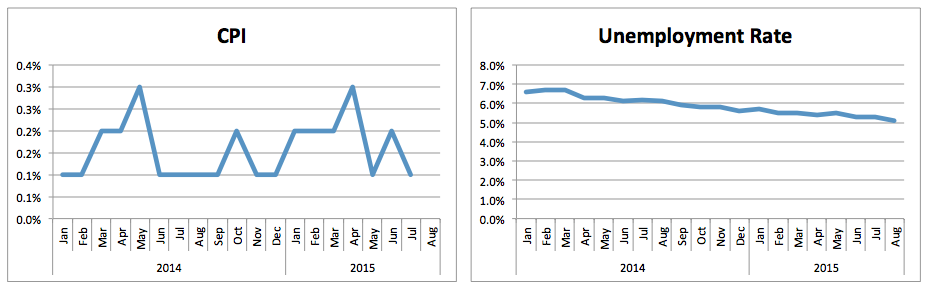
Therefore, the main role of Fed is to conduct the monetary policy by manipulating the federal funds rate, which is the three-month short-term interest rate. This monetary policy is very crucial to the health of today’s economy. It is often known as the Fed’s dual mandate: price stability and maximum employment. There is always a trade off between inflation rate and unemployment rate according to the Phillips curve. When inflation rate is high, unemployment rate is low, vice versa. Thus, the Fed wants to cool down economy by manipulating a monetary policy to lower inflation rate in order to stabilize the price level while unemployment rate may rise. Today’s economy on the other hand is experiencing low inflation thanks to lower gas prices as well as global economic slowdown. The Fed wants to normalize the price level to be around 2 percent, which the former Fed Chairman, Ben Bernanke, calls, “buffer zone,” where the Fed can comfortably manipulates the economy by adjusting the federal funds rate. In the meantime, the economy is nearing full employment while the unemployment rate has successfully improved from over 10 percent in 2009-2010 to today’s 5.3 percent (Though employment structure has changed since the post financial crisis but the number is at least healthy). Thus, the Fed so far has successfully achieved one part of the dual mandate.
(L) Consumer Price Index and (R) Unemployment Rate in the United States during 2014-2015. | Source: Bureau of Labor Statistics
The other part of the dual mandate, price stability, is the one that the Fed now has to focus on. At zero interest policy, like in today’s economy, the Fed really has to avoid the economy falling into a deflationary period. Japan has been in a deflationary period for past 20 years and that 20-year period is often called, Japan’s “lost 20 years.” Under such deflationary period, the price level kept falling, causing Japan’s economy into a prolonged recession. With such lesson from Japan, the Fed has stimulated the economy by several rounds of quantitative easing (QE) in the past years.
Three Tools + QE
In fact, QE is a type of an unconventional monetary policy that buys significant amount of financial assets, such as corporate bonds, from private banks while an ordinal monetary policy buys or sells short-term government bonds through an open market operation (OMO). Since the short-term interest rates have been at zero since very end of 2008, this OMO, a primary method of implementing monetary policy, no longer worked. The other tools to stimulate the economy are: discount rate and reserve requirement. The discount rate is the interest rate that the Fed directly charges to commercial banks for short-term loans. That is where the term, “lender of the last resort,” comes from. When commercial banks are in trouble and a troubled bank no longer able to borrow money from the other commercial banks, the bank has to step into the Fed building directly to borrow money. That means lower the discount rate, easier the commercial banks to able to borrow money at lower cost. However, the discount rate should be slightly higher than the interbank rates, meaning borrowing cost from the Fed is slightly higher than that from the other commercial banks. On the other hand, the reserve requirement is set on the banks’ balance sheets. Like your checking account at Bank of America or other commercial banks, you have a minimum balance requirement to hold in order to avoid a maintenance fee. Similar to this, commercial banks also have a minimum cash deposit requirement set by the Fed. That means lower the reserve requirement is, more flexibility that commercial banks have. Therefore, the Fed manipulates those three conventional tools to achieve its monetary policy goals. A decrease in OMO, discount rate, or reserve requirement simply indicates the Fed is conducting the expansionary monetary policy, and vice versa.
<Next Page - Money> |
<Next Page><Previous Page>Federal Funds Rate
|
